Very Large Scale Integration (VLSI)
VLSI Encyclopedia - Connecting VLSI Engineers
Featured post
Top 5 books to refer for a VHDL beginner
VHDL (VHSIC-HDL, Very High-Speed Integrated Circuit Hardware Description Language) is a hardware description language used in electronic des...
Tuesday 15 June 2021
Top 5 books to refer for a VHDL beginner
Monday 7 June 2021
Effective VIM Editor tips, tricks and plugins to improve coding speed in VLSI
One of our colleagues always had to struggle with the Verilog / SystemVerilog syntax. Whenever he opens a .sv file he needs to set the syntax manually as ":set syntax=verilog". This really kills time, especially when you are working on a project with tight schedules.
Opening a fine using GVIM
Shortcuts for moving the cursor:
Shortcuts for quick editing:
How do I switch between panes in a split mode in Vim/GVIM ??
How to remove blank lines from a file?
How to implement AUTO-COMPLETION
Tuesday 4 May 2021
UVM Interview Questions - 6
Q36: What is the Difference between UVM_ALL_ON and UVM_DEFAULT?
UVM_ALL_ON and UVM_DEFAULT are identical. As per the UVM reference manual:UVM_ALL_ON: Set all operations on (default).
UVM_DEFAULT: Use the default flag settings.
Q37: What drain time in UVM?
class test_base extends uvm_test; // ... function void end_of_elaboration_phase(uvm_phase phase); uvm_phase main_phase = phase.find_by_name("main", 0); main_phase.phase_done.set_drain_time(this, 10); endfunction // ... endclass
Q38: What is Virtual interface and how Virtual interface is used?
module top;…dut_if dif;…initial beginuvm_config_db#(virtual dut_if)::set(null, "*", "vif", dif);run_test();endendmoduleclass tb_driver extends uvm_driver #(trans1);…virtual dut_if vif;…function void build_phase(uvm_phase phase);super.build_phase(phase);// Get the virtual interface handle that was stored in the// uvm_config_db and assign it to the local vif field.if (!uvm_config_db#(virtual dut_if)::get(this, "", "vif", vif))`uvm_fatal("NOVIF", {"virtual interface must be set for: ",get_full_name(), ".vif"});endfunction…endclass
Q39: How to add a user-defined phase in UVM?
If needed a user can create user-defined phases in the UVM environment. However, this may impact the re-usability of the component. To define a custom phase user need to extend the appropriate base class for phase-type. Following are the available base classes.
class my_phase extends uvm_task_phase;
class my_phase extends uvm_topdown_phase;
class my_phase extends uvm_bottomup_phase;
You can refer to the UVM PHASE IMPLEMENTATION EXAMPLE for complete user-defined phase understanding.
Q40: How interface is passed to components in UVM?
Monday 10 August 2020
Useful Vim plug-in for efficient coding in Perl
- Auto addition of file header
- Easy addition of function/frame comment
- Quick inclusion of default code snippet
- Performing syntax check
- Reading documentation about a function
- Converting a full code block to comment, and vice versa
- Help to speed up the code writing with consistency in coding.
The Perl-Support Vim Plugin – Perl-IDE offers the easiest way to do all of the above, saving a lot of time and keystrokes.
We have already discussed in an earlier article regarding Use of Scripting languages in VLSI
We will be covering the following in this article
1. How to install perl-support plugin to use it with VIM.
2. Powerful features of the Perl-support plugin.
Steps to install Perl-Support VIM Plug-in
1. Download the plugin from the vim.org website.
Click here to download to go to the download page
Alternatively use below command
cd /usr/src/
wget http://www.vim.org/scripts/download_script.php?src_id=9701
2. Copy the zip archive perl-support.zip to $HOME/.vim and run below command
unzip perl-support.zip
This command will create following files:
$HOME/.vim/autoload/mmtemplates/...
$HOME/.vim/doc/...
$HOME/.vim/plugin/perl-support.vim
3. Loading of plug-in files must be enabled in $HOME/.vimrc. If not use previously
filetype plugin on
Create .vimrc if there is none or use the files in $HOME/.vim/perl-support/rc as a starting point.
After done with installation lets get to know about
The Powerful Features of Perl-support
1. Add Automatic Header to *.pl file whenever you create a new file
2. Insert statements
3. Insert frequently used statements
4. Insert special variables
5. insert code snippets and manage templates
6. Run a profiler
7. Run the script, check the syntax, start the debugger
8. Make integration
Thursday 6 August 2020
Use of Scripting languages in VLSI
- Front end RTL/Testbench code compilation and simulation flows
- Automation of running tests in regressions, generating reports, analyzing failures, debug automation
- Connectivity checks, netlist parsing, automatic generation/modification any RTL module/stubs, etc
- Synthesis, P&R tools interfacing, and back end flow.
- Several project management utilities - regression pass rates, trends, bug charts, etc - that helps in tracking projects
- Any other task that is repetitive in workflow and can be automated.
Monday 3 August 2020
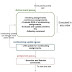
UPF - Unified Power Format
What is UPF?
When does it started?
How to use UPF in design?
Who supports it?
The below flow shows the stages of design flow and where UPF is used.
Thursday 2 April 2020
Understanding Logic gates at transistor level : Not Gate
The input of the NOT Gate is connected at the base of the transistor and the output is taken from the collector. The transistor here acts as the switch so when the voltage is applied at the base of the transistor the transistor starts conducting and shorts the output to the ground similarly when no voltage is applied at the input the output is connected to the Vcc as shown thus in this way the circuit implements the NOT function.
-
This post will help you to understand the difference between real, realtime and shortreal data types of SystemVerilog and its usage. ...
-
In Verilog certain type of assignments or expression are scheduled for execution at the same time and order of their execution is not guara...
-
Very often we come across questions from VLSI engineers that "Which scripting language should a VLSI engineer should learn?". Well...
-
VHDL (VHSIC-HDL, Very High-Speed Integrated Circuit Hardware Description Language) is a hardware description language used in electronic des...
-
In previous post of this SystemVerilog Tutorial we talked about enumerated type in detail. Now we will look at the constants in SystemVe...